4 minutes
Written: 2021-09-25 00:00 +0000
Basics of GANs and Loss Function
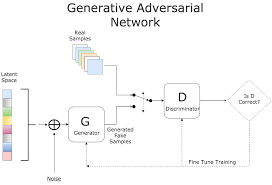
GANs are deep neural architecture trained in an adversarial manner (in english dictionary, adversarial means conflict or opposition) to generate data that mimics the distribution we want to approximate. It comprises of two networks - Generator and Discriminator, competing one against the other (that is why Adversarial).
-
Discriminator
It discriminates between two different classes of data, that is why known as binary classifier. For exampe when you want to classify real and fake images of person, then discriminative network comes into use. The output of these will be either 0 or 1 (0 - when it is fake and 1 - when its real). The role of discriminator is to discriminate between two different classes and produce the result as fake(0) or not fake(1).
-
Generator
The generator part of a GAN creates fake data by incorporating feedback from the discriminator. The portion of the GAN that trains the generator includes:
- Random input
- Generator network, which transforms the random input into a data instance
- Discriminator network, which classifies the generated data
- Discriminator output generator loss, which penalizes the generator for failing to fool the discriminator.
LOSS FUNCTION
The role of discriminator is to recognize an image as fake(image generated from generator) or real image accurately. It should produce 1 for real disributiom and 0 for generated distributions. While, generator generates images similar to the sample data distribution such that discriminator cannot distinguish it with the original data.
Once the generator produces correct classification, back propogation will be done as generator fails to fool the discriminator so its an error, this back-propogation will adjust the weights and biases of generator network. When the weights and biases gets adjusted, the generator will again generate samples from these distributions, this time making hard for the discriminator to classify real and generated distributions. This process goes on until the discriminator fails to classify between real and fake distributions.
First of all, lets get familiar with the mathematical terms -
- Pdata(x): Probablity distribution of the sample dataset (our objective is to approximate this Pdata(x) through generator function)
- x: instantiation of random variable X.These x are fed into D(x,theta1) produces transformed variable represented as D(X). D(X) represents the probability that X is basically coming from the original dataset. D(X) have range between 0 and 1.
- pZ(z): Random distribution
- z: samples generated by random noise. z feded into generator which is a neural network takes input as z and parametrize by theta2, G(z, theta2) theta2 will represnt the weights and biases for the neural network represented by generator network which will be adjusted during the back propogation produces transformed variable represented as G(z).
NOTE: G and D are differentiable functions( once you are doing the back-propogation, it should be easily differentiable)
- pg(x): Probability distribution of dataset generated from generator.
OBJECTIVE :
pg(x) = pdata(x)
When G(z) is fed into the discriminator, it produces the probability represented as D(G(z)) which ranges between 0 and 1.
A generative model G to be trained on training data X sampled from some true distribution D is the one which given some random distribution Z produces D’ close to D according to some closeness metric. Mathematically z~Z maps to a sample G(z) ~ D'(Generative samples in D').
Binary cross entropy loss function is given as -
L(ypred, y) = y log(ypred) + (1-y) log(1-ypred)
where, ypred = reconstructed image, y = original image
The labels for the data coming from original data distribution ie. pdata(x) is y=1 (real dataset) and the reconstructed labels ypred = D(X).
L(D(X),1) = log(D(X))
For the data coming from generator the label is y=0 (fake dataset) and ypred = D(G(X)) so in that case
L(D(G(z)),0) = log(1-D(G(z))
- D(x) = Discriminator activation applied directly to the actual input data.
- D(G(z)) = Discriminator activation applied to the generated data
Since the objective of the discriminator is to currently classify fake vs real dataset. For this reason eqn 1 and 2 must be maximized. (Can be visualized more by drawing graphs of these two eqns)
D = max{log(D(x)+log(1-D(G(z)))}
Since the objective of the generator is to fool the discriminator that means it wants D(G(z)) = 1. This means we need to minimize the objective function.
G = min{log(D(x))+log(1-D(G(z)))}
So during the game between generator and discriminator, the target of D(Discriminator) is to maximize the above cost function while G(Generator) tries to minimize. By combining both these objectives, we can write the final equation as,
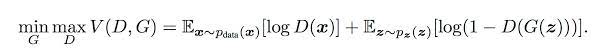
This was all about the basics of GAN and its loss functions. I will discuss more about implementation of GANs in my next blog.
Thanks for reading!
